A polygon is a figure formed by line segments which bound a portion of the plane (Figure \(\PageIndex\)), The bounding line segments are called the sides of the polygon, The angles formed by the sides are the angles of the polygon and the vertices of these angles are the vertices of the polygon, The simplest polygon is the triangle, which has 3 sides, In this chapter we will study the quadrilateral, the polygon with 4 sides (Figure \(\PageIndex\)). Other polygons are the pentagon (5 sides), the hexagon (6 sides), the octagon (8 sides), and the decagon (10 sides).
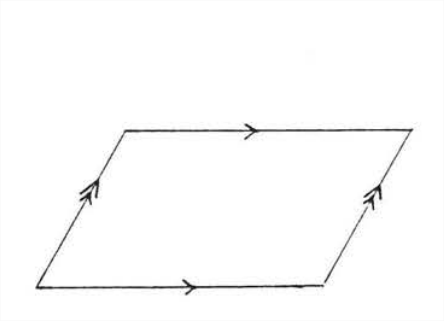
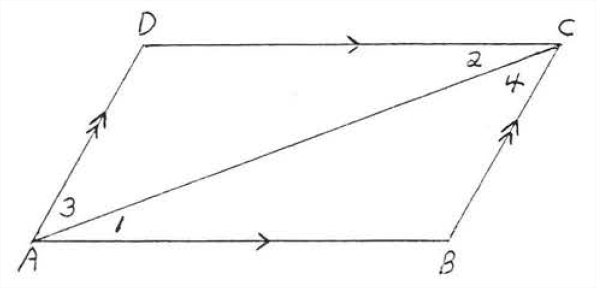
A parallelogram is a quadrilateral in which the opposite sides are parallel (Figure \(\PageIndex\)). To discover its properties, we will draw a diagonal, a line connecting the opposite vertices of the parallelogram. In Figure 4, AC is a diagonal of parallelogram \(ABCD\). We will now prove \(\Delta ABC \cong \Delta CDA\).
| Statements | Reasons |
|---|---|
| 1. \(\angle 1 = \angle 2\). | 1. The alternate interior angles of parallel lines \(AB\) and \(CD\) are equal. |
| 2. \(\angle 3 = \angle 4\). | 2. The alternate interior angles of parallel lines \(BC\) and \(AD\) are equal. |
| 3. \(AC = AC\). | 3. Identity. |
| 4. \(\triangle ABC \cong \triangle CDA\). | 4. \(ASA = ASA\). |
| 5. \(AB = CD\), \(BC = DA\). | 5. The corresponding sides of congruent triangles are equal. |
| 6. \(\angle B = \angle D\). | 6. The corresponding angles of congruent triangles are equal. |
| 7. \(\angle A = \angle C\). | 7. \(\angle A = \angle 1 +\angle 3 = \angle 2 + \angle 4 = \angle C\) (Add statements 1 and 2). |
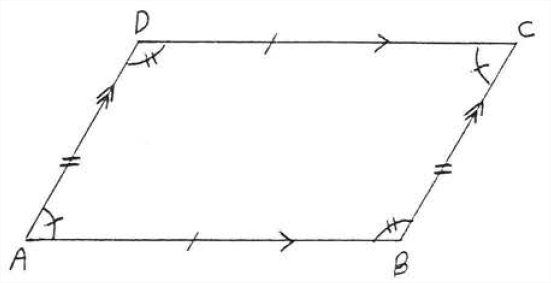
In parallelogram \(ABCD\) of Figure \(\PageIndex<5>\), \(AB = CD\), \(AD = BC\), \(\angle A = \angle C\), and \(\angle B = \angle D\).
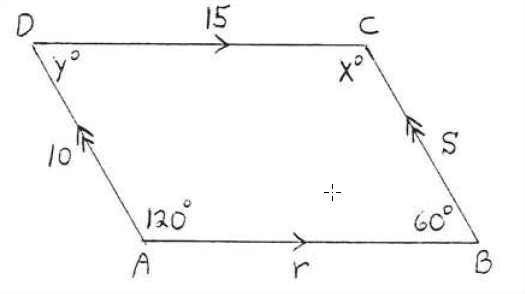
Find \(x\), \(y\), \(r\) and \(s\): Solution By Theorem \(\PageIndex\) , the opposite sides and opposite angles are equal. Hence \(x^ = 120^\), \(y^ = 60^, r = 15\), and \(s = 10\). Answer: \(x = 120, y = 60, r = 15, s = 10\).
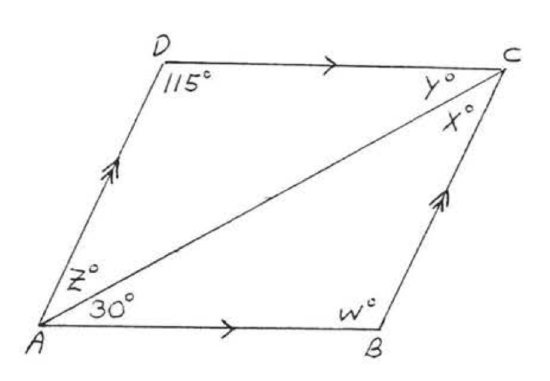
Find \(x, y, x\) and \(z:\) Solution \(w^ = 115^\) since the opposite angles of a parallelogram are equal. \(x^ = 180^ -(w^ + 30^) = 180^ - (115^ + 30^) = 180^ - 145^ = 35^\), because the sum of the angles of \(\triangle ABC\) is \(180^\), \(y^ = 30^\) and \(x^ = x^ = 35^\) because they are alternate interior angles of parallel lines. Answer: \(w = 115\), \(x = z = 35\), \(y = 30\).
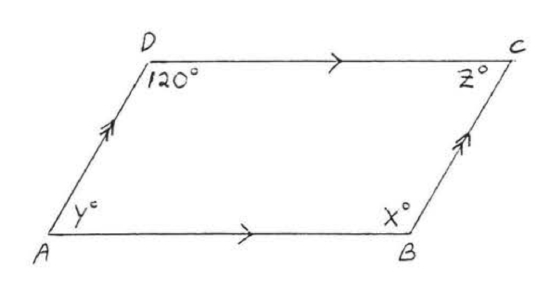
Find \(x\), \(y\), and \(z\): Solution \(x = 120\) and \(y = z\) because the opposite angles are equal, \(\angle A\) and \(\angle D\) are supplementary J because they are interior angles on the same side of the transversal of parallel lines (they form the letter "C." Theorem \(\PageIndex\), section 1.4). Answer: \(x = 120, y = z = 60\).
In Example \(\PageIndex<3>\), \(\angle A\) and \(\angle B\), \(\angle B\) and \(\angle C\), \(\angle C\) and \(\angle D\), and \(\angle D\) and \(\angle A\) are called the successive angles of parallelogram \(ABCD\). Example \(\PageIndex<3>\) suggests the following theorem:
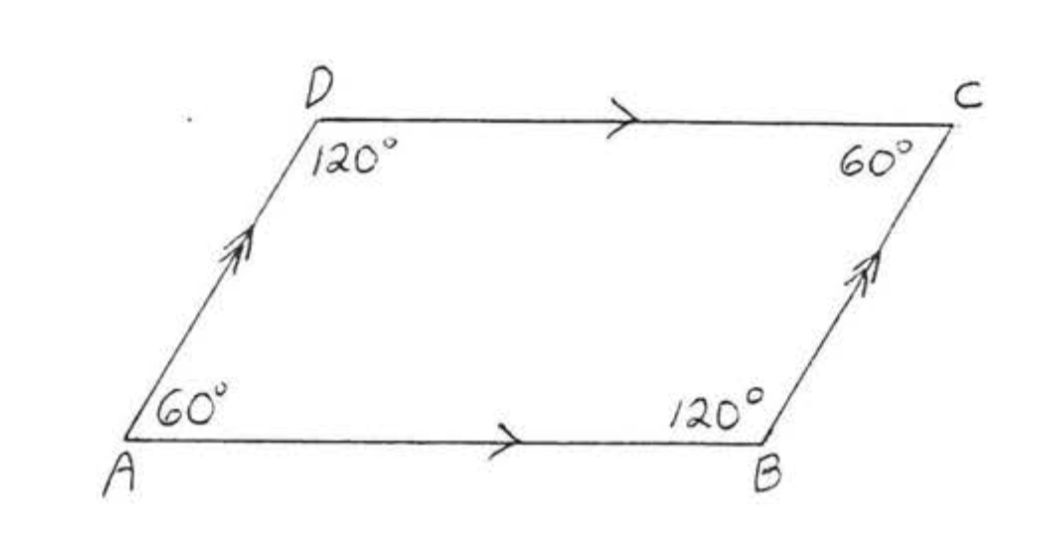
In Figure 6,\(\angle A + \angle B = \angle B + \angle C = \angle C + \angle D = \angle D + \angle A = 180^\).
Find \(x\), \(\angle A\), \(\angle B\), \(\angle C\), and \(\angle D\).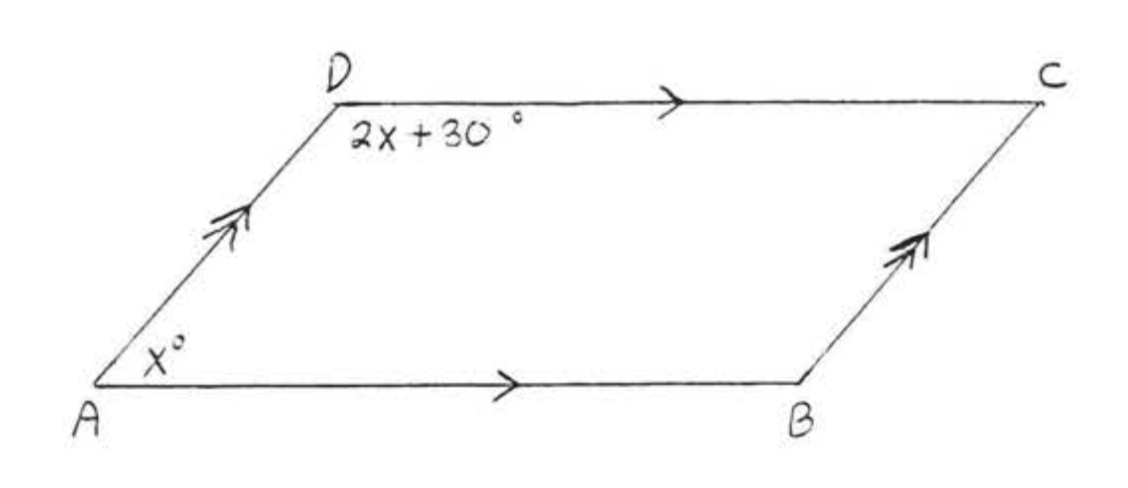 
Solution \(\angle A\) and \(\angle D\) are supplementary by Theorem \(\PageIndex\). \[\begin & = & > \\ & = & \\ & = & \\ & = & \\ & = & \\ & = & \end\] \(\angle A = x^ = 50^\) \(\angle C = \angle A = 50^\) \(\angle D = 2x + 30^ = 2(50) + 30^ = 100 + 30^ = 130^\). \(\angle B = \angle D = 130^\). Check: 
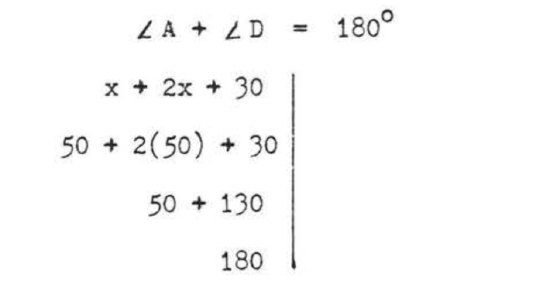Answer: \(x = 50\), \(A = 50^\), \(B = 130^\), \(C = 50^\), \(D = 130^\).
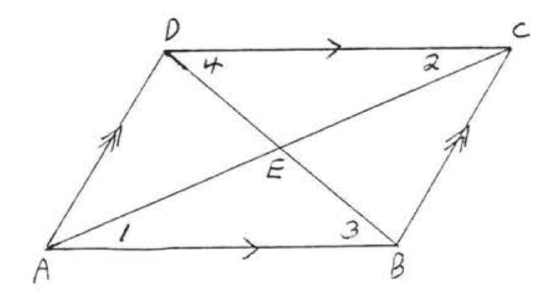
Suppose now that both diagonals of parallelogram are drawn (Figure \(\PageIndex<7>\) ): We have \(\angle 1 = \angle 2\) and \(\angle 3 = \angle 4\) (both pairs of angles are alternate interior angles of parallel lines \(AB\) and \(CD\). Also \(AB = CD\) from Theorem \(\PageIndex\). Therefore \(\triangle ABE \cong \triangle CDE\) by \(ASA = ASA\). Since corresponding sides of congruent triangles are equal, \(AE = CE\) and \(DE = BE\). We have proven:
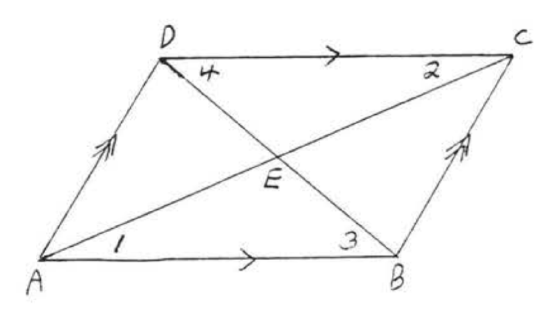
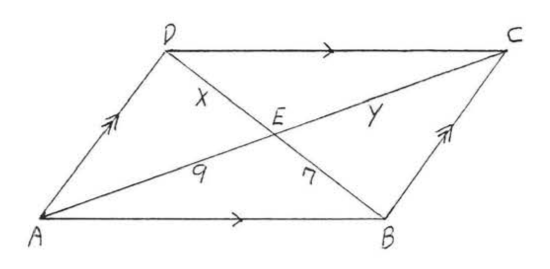
Find \(x, y, AC\), and \(BD\): Solution By Theorem \(\PageIndex\) the diagonals bisect each other. \[\begin & = & \\ & = & \\ & = & \\ & = & \end\] Answer: \(x = 7, y = 9, AC = 18, BD = 14\).
Find \(x, y, AC\), and \(BD\):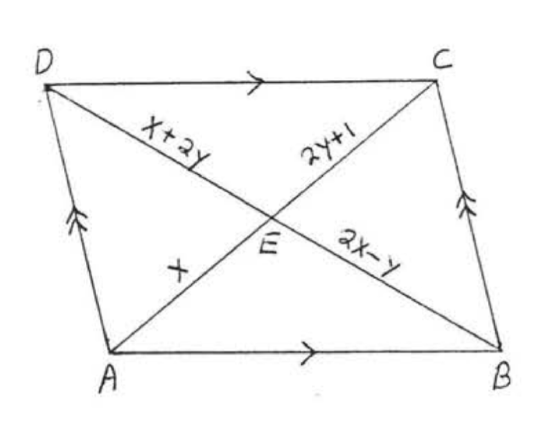 
Solution By Theorem \(\PageIndex\) the diagonals bisect each other. \(\begin & = & \\ & = & \\ & = & \end\) \(\begin & = & \\ & = & \\ & = & \\ & = & \end\) 
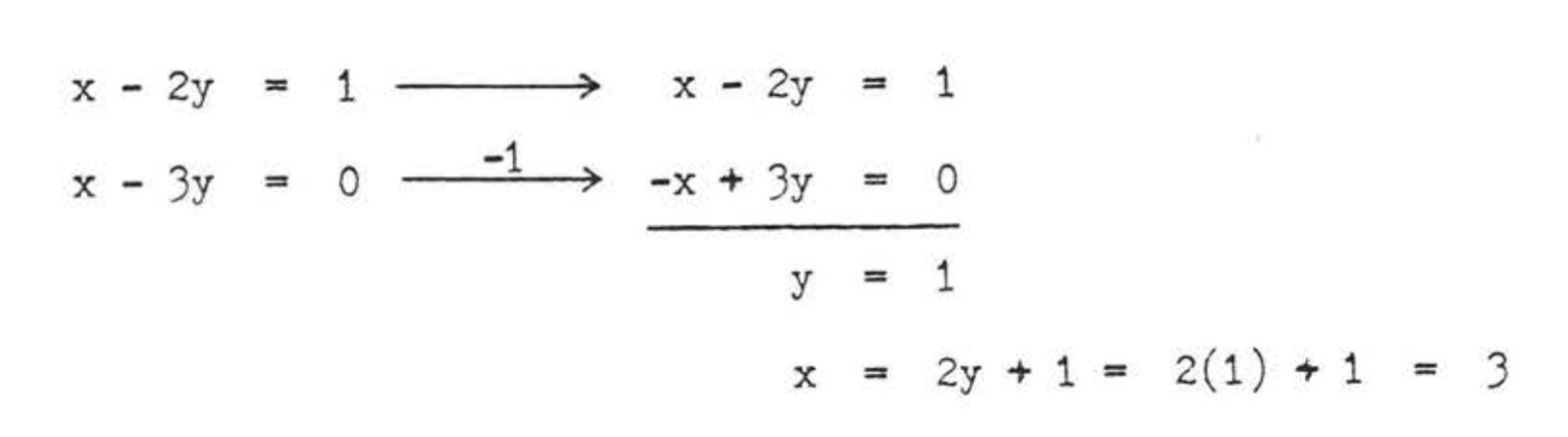Check: 
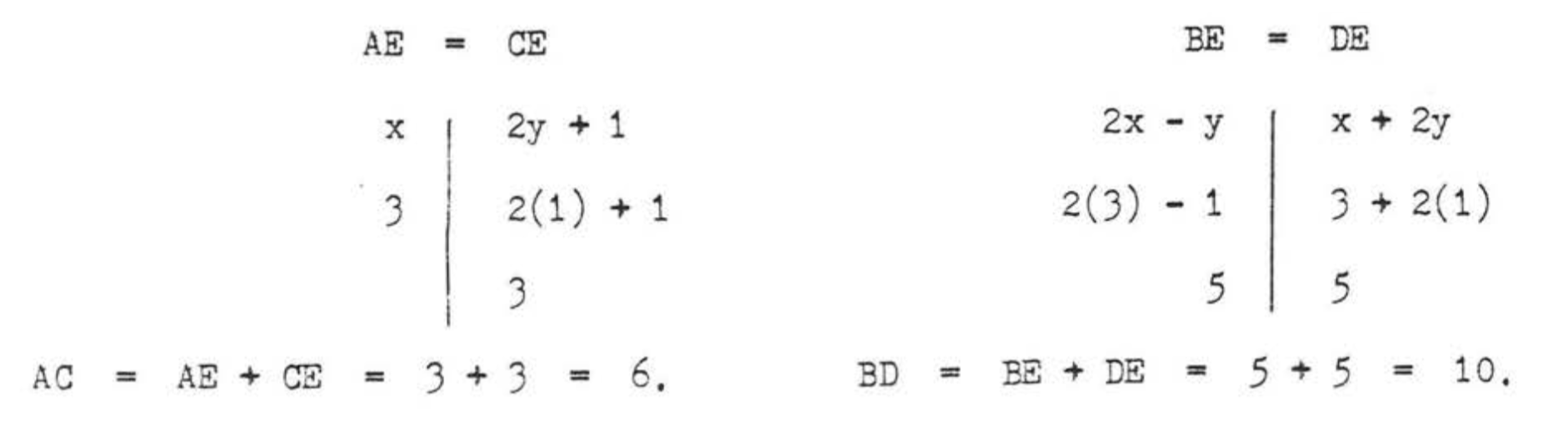Answer: \(x = 3, y = 1, AC = 6, BD = 10\).
Find \(x, y, \angle A, \angle B, \angle C\), and \(\angle D\):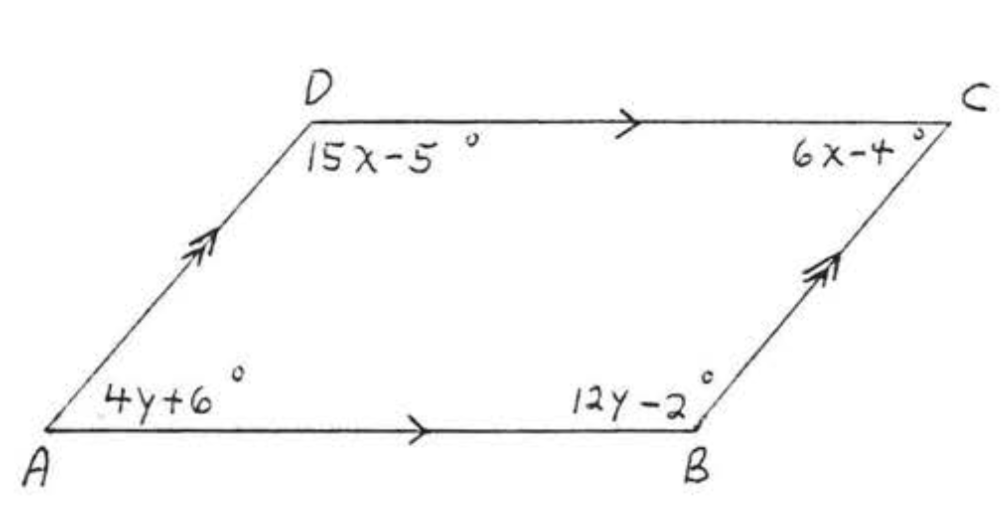 
Solution By Theorem \(\PageIndex\): \(\begin & = & > \\ & = & \\ & = & \\ & = & \\ & = & \\ & = & \end\) and \(\begin & = & > \\ & = & \\ & = & \\ & = & \\ & = & \\ & = & \end\) Check: 
Answer: \(x = 9, y = 11, \angle A = \angle C = 50^, \angle B = \angle D = 130^\).
For each of the following state any theorem used in obtaining your answer(s): 1. Find \(x, y, r\), and \(s\):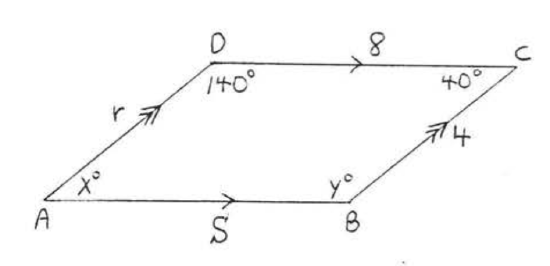 
2. Find \(x, y, r\), and \(s\): 
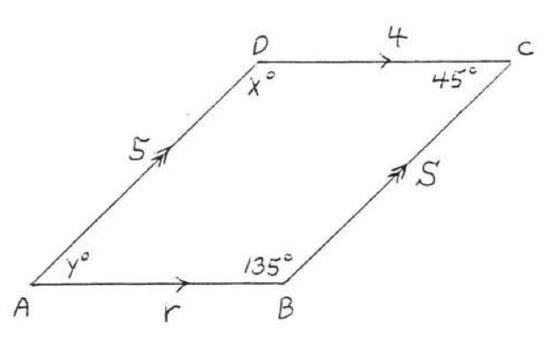3. Find \(w, x, y\), and \(z\): 
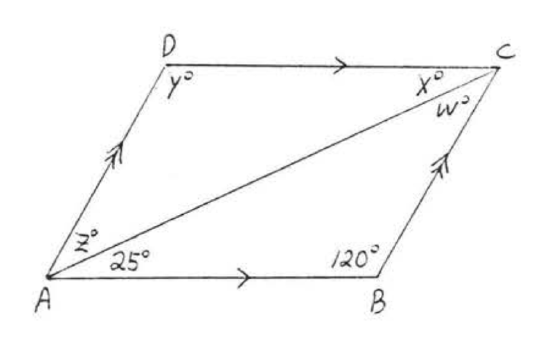4. Find \(w, x, y\), and \(z\): 
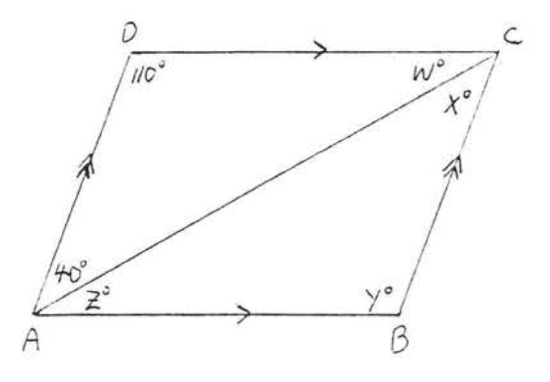5. Find \(x, y\), and \(z\): 
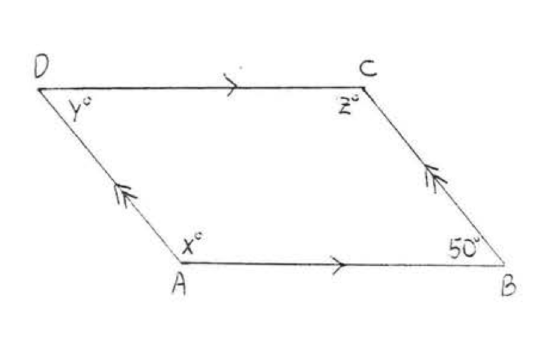6. Find \(x, y\), and \(z\): 
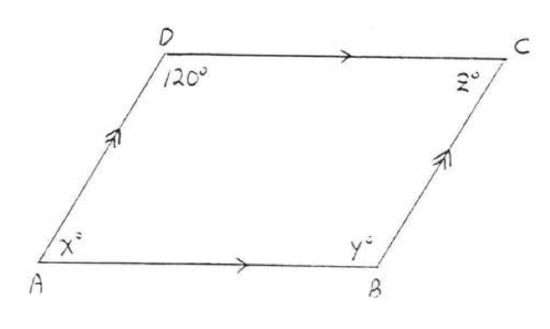7. Find \(x, \angle A, \angle B, \angle C\), and \(\angle D\): 
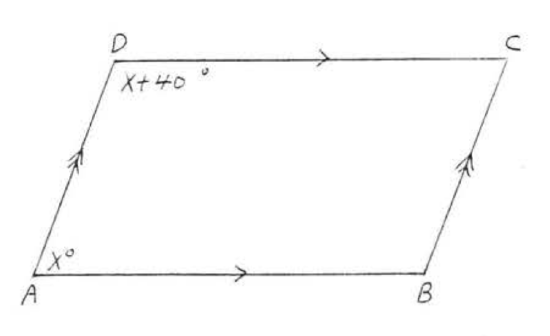8. Find \(x, \angle A, \angle B, \angle C\), and \(\angle D\): 
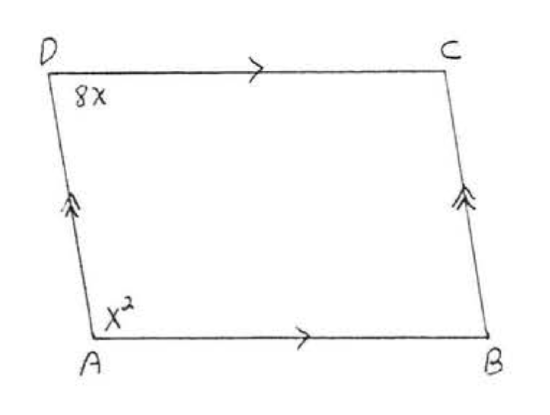9. Find \(x, y, AC\), and \(BD\): 
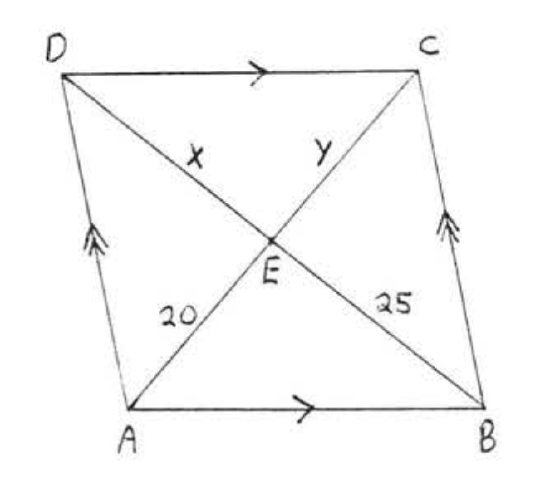10. Find \(x, y, AC\), and \(BD\): 
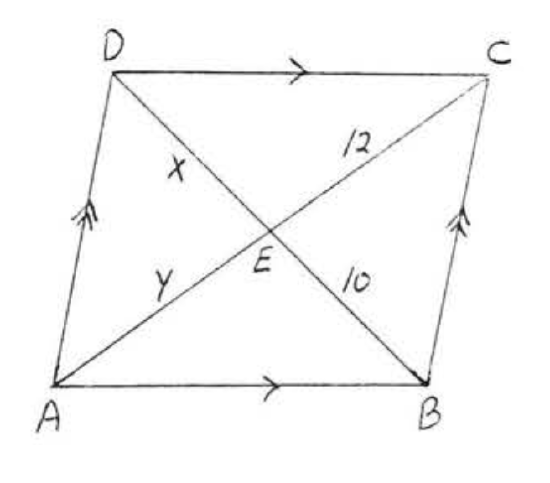11. Find \(x, AB\), and \(CD\): 
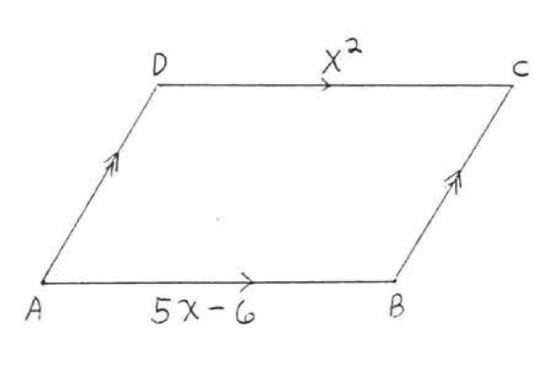12. Find \(x, AD\), and \(BC\): 
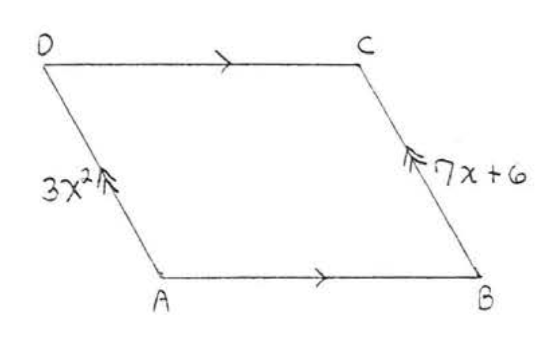13. Find \(x, y, AB, BC, CD\), and \(AD\): 
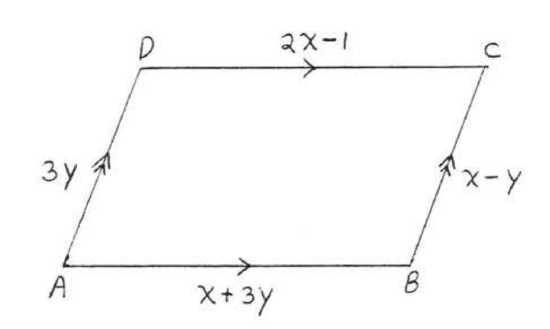14. Find \(x, y, AB, BC, CD\), and \(AD\): 
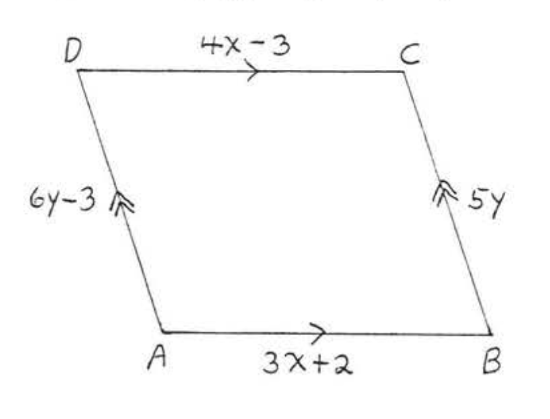15. Find \(x, y, AC\), and \(BD\): 
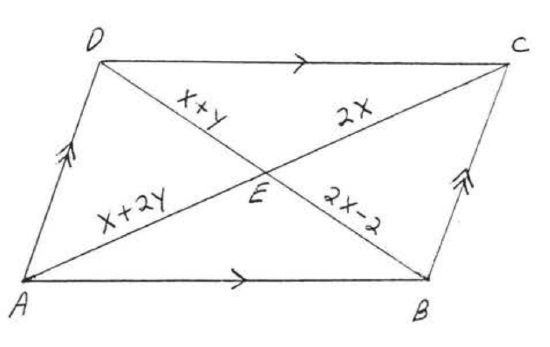16. Find \(x, y, AC\), and \(BD\): 
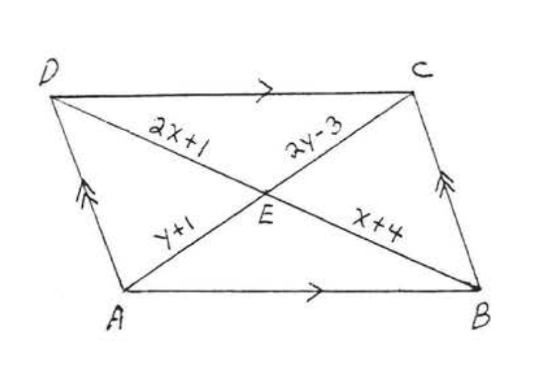17. Find \(x, y, \angle A, \angle B, \angle C\), and \(\angle D\): 
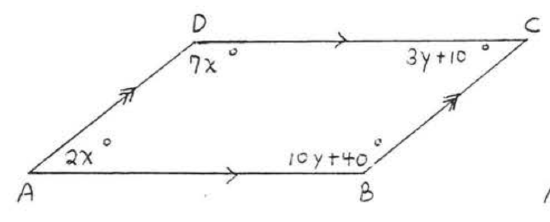18. Find \(x, y, \angle A, \angle B, \angle C\), and \(\angle D\):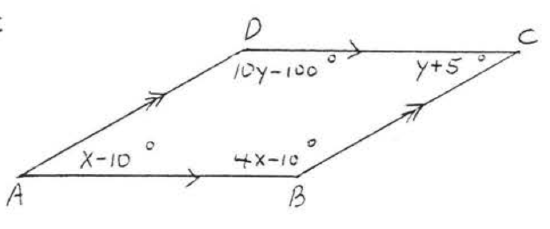 
This page titled 3.1: Parallelograms is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Henry Africk (New York City College of Technology at CUNY Academic Works) via source content that was edited to the style and standards of the LibreTexts platform.
